𝐈𝐍𝐓𝐑𝐎𝐃𝐔𝐂𝐓𝐈𝐎𝐍 𝐓𝐎 𝐀𝐋𝐆𝐎𝐑𝐈𝐓𝐇𝐌𝐒

Disclaimer

The solution of question or notes are written by either student or taken from some publications , so it is the responsibility of viewer to check whether answers are correct or incorrect.

Definition: -

An algorithm is a Step By Step process to solve a problem, where each step indicates an intermediate task. Algorithm contains finite number of steps that leads to the solution of the problem.

Characteristics of an Algorithm:-

Algorithm has the following basic properties

• Input-Output:- Algorithm takes ‘0’ or more input and produces the required output. This is the basic characteristic of an algorithm.

• Finiteness:- An algorithm must terminate in countable number of steps.

• Definiteness: Each step of an algorithm must be stated clearly and unambiguously.

• Effectiveness: Each and every step in an algorithm can be converted in to programming language statement.

• Generality: Algorithm is generalized one. It works on all set of inputs and provides the required output. In other words it is not restricted to a single input value.

Categories of Algorithm:

Based on the different types of steps in an Algorithm, it can be divided into three categories, namely

1. Sequence

2. Selection and

3. Iteration

Sequence:- The steps described in an algorithm are performed successively one by one without skipping any step. The sequence of steps defined in an algorithm should be simple and easy to understand. Each instruction of such an algorithm is executed, because no selection procedure or conditional branching exists in a sequence algorithm.

Example:

// adding two numbers

Step 1: start

Step 2: read a,b

Step 3: Sum=a+b

Step 4: write Sum

Step 5: stop

Selection: The sequence type of algorithms are not sufficient to solve the problems, which involves decision and conditions. In order to solve the problem which involve decision making or option selection, we go for Selection type of algorithm. The general format of Selection type of statement is as shown below:

if(condition)

Statement-1;

else

Statement-2;

The above syntax specifies that if the condition is true, statement-1 will be executed otherwise statement-2 will be executed. In case the operation is unsuccessful. Then sequence of algorithm should be changed/ corrected in such a way that the system will re- execute until the operation is successful.

Iteration:- Iteration type algorithms are used in solving the problems which involves

repetition of statement. In this type of algorithms, a particular number of statements

are repeated ‘n’ no. of times.

Example1:

Step 1 : start

Step 2 : read n

Step 3 : repeat step 4 until n>0

Step 4 : (a) r=n mod 10 (b) s=s+r (c) n=n/10

Step 5 : write s

Step 6 : stop

Performance Analysis an Algorithm:-

The Efficiency of an Algorithm can be measured by the following metrics.

i. Time Complexity and

ii. Space Complexity.

i.Time Complexity:-

The amount of time required for an algorithm to complete its execution is its time

complexity. An algorithm is said to be efficient if it takes the minimum (reasonable)

amount of time to complete its execution.

ii. Space Complexity:-

The amount of space occupied by an algorithm is known as Space Complexity. An

algorithm is said to be efficient if it occupies less space and required the minimum

amount of time to complete its execution

1.Write an algorithm for roots of a Quadratic Equation?

// Roots of a quadratic Equation

Step 1 : start

Step 2 : read a,b,c

Step 3 : if (a= 0) then step 4 else step 5

Step 4 : Write “ Given equation is a linear equation “

Step 5 : d=(b * b) _ (4 *a *c)

Step 6 : if ( d>0) then step 7 else step8

Step 7 : Write “ Roots are real and Distinct”

Step 8: if(d=0) then step 9 else step 10

Step 9: Write “Roots are real and equal”

Step 10: Write “ Roots are Imaginary” Step 11: stop

2. Write an algorithm to find the largest among three different numbers entered by user

Step 1: Start

Step 2: Declare variables a,b and c.

Step 3: Read variables a,b and c.

Step 4: If a>b If a>c

Display a is the largest

number.

Else

Display c is the largest number.

Else

If b>c

Display b is the largest

number. Else

Display c is the greatest number.

Step 5: Stop

ASYMPTOTIC NOTATIONS : -

Asymptotic analysis of an algorithm refers to defining the mathematical

boundation/framing of its run-time performance. Using asymptotic analysis, we can

very well conclude the best case, average case, and worst case scenario of an

algorithm.

Asymptotic analysis is input bound i.e., if there's no input to the algorithm, it is

concluded to work in a constant time. Other than the "input" all other factors are

considered constant.

Asymptotic analysis refers to computing the running time of any operation in

mathematical units of computation. For example, the running time of one operation

is computed as f(n) and may be for another operation it is computed as g(n2). This

means the first operation running time will increase linearly with the increase in n

and the running time of the second operation will increase exponentially when n 5

increases. Similarly, the running time of both operations will be nearly the same if n

is significantly small

The time required by an algorithm falls under three types -

• Best Case - Minimum time required for program execution.

• Average Case - Average time required for program execution.

• Worst Case - Maximum time required for program execution.

Asymptotic Notations

Following are the commonly used asymptotic notations to calculate the running

time complexity of an algorithm.

• Ο Notation

• Ω Notation

• θ Notation

Big Oh Notation, Ο

The notation Ο(n) is the formal way to express the upper bound of an algorithm's

running time. It measures the worst case time complexity or the longest amount of

time an algorithm can possibly take to complete

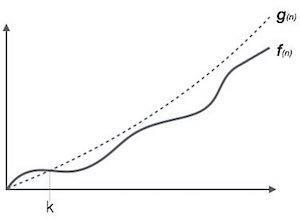
For example, for a function f(n)

Ο(f(n)) = { g(n) : there exists c > 0 and n0 such that f(n) ≤ c.g(n) for all n > n0. }

Omega Notation, Ω

The notation Ω(n) is the formal way to express the lower bound of an algorithm's

running time. It measures the best case time complexity or the best amount of time

an algorithm can possibly take to complete

For example, for a function f(n)

Ω(f(n)) ≥ { g(n) : there exists c > 0 and n0 such that g(n) ≤ c.f(n) for all n > n0. }

Theta Notation, θ

The notation θ(n) is the formal way to express both the lower bound and the upper

bound of an algorithm's running time. It is represented as follows

θ(f(n)) = { g(n) if and only if g(n) = Ο(f(n)) and g(n) = Ω(f(n)) for all n > n0. }